Parabolic Lie algebra

In algebra, a parabolic Lie algebra 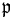$\mathfrak p$ is a subalgebra of a semisimple Lie algebra 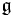$\mathfrak g$ satisfying one of the following two conditions:

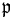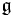$\mathfrak p$ contains a maximal solvable subalgebra (a Borel subalgebra) of $\mathfrak g$ ;
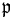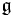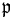the Killing perp of $\mathfrak p$ in $\mathfrak g$ is the nilradical of $\mathfrak p$ .

These conditions are equivalent over an algebraically closed field of characteristic zero, such as the complex numbers. If the field 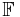$\mathbb F$ is not algebraically closed, then the first condition is replaced by the assumption that

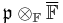$\mathfrak p\otimes_{\mathbb F}\overline{\mathbb F}$ contains a Borel subalgebra of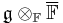 $\mathfrak g\otimes_{\mathbb F}\overline{\mathbb F}$

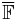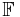where $\overline{\mathbb F}$ is the algebraic closure of $\mathbb F$ .

Bibliography

Baston, Robert J.; Eastwood, Michael G. (1989), The Penrose Transform: its Interaction with Representation Theory, Oxford University Press .
Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics, 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR 1153249, ISBN 978-0-387-97527-6
Grothendieck, Alexander (1957), "Sur la classification des fibrés holomorphes sur la sphère de Riemann", Amer. J. Math. 79 (1): 121–138, doi:10.2307/2372388, JSTOR 2372388 .
Humphreys, J. (1972), Linear Algebraic Groups, New York: Springer, ISBN 0-387-90108-6

Parabolic Lie algebra

See also

Bibliography